skcho 님의 블로그

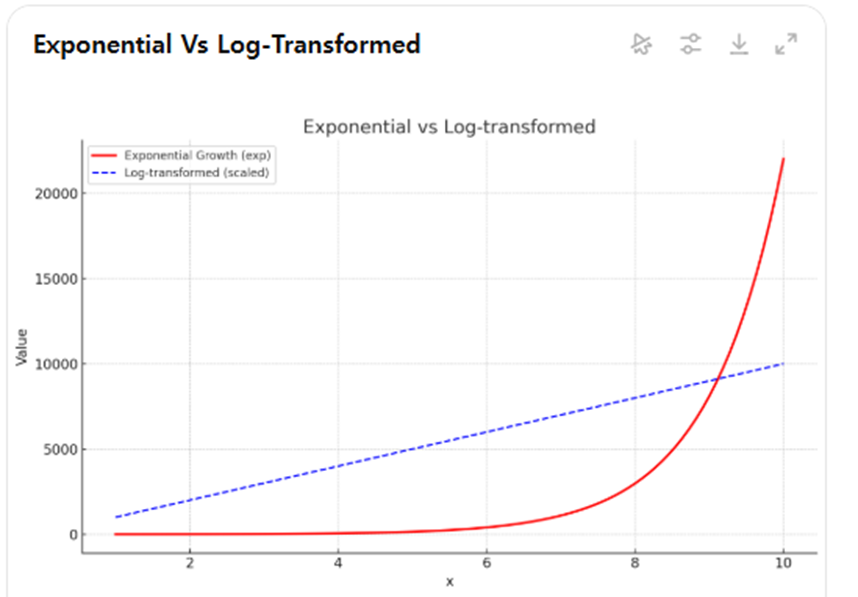
회귀분석을 할 때 연속형 변수는 대개 별다른 가공 없이 그대로 분석에 사용한다.그러나 값의 범위가 너무 크거나, 분포가 한쪽으로 심하게 치우쳐 있는 경우에는 그대로 사용하기에 적합치 않다.이런 변수를 그대로 쓰면 회귀모형의 가정을 위배하거나, 결과 해석이 왜곡될 수 있다.예를 들어, 도시 인구, 기업 매출, 가구소득처럼 일부 극단적으로 큰 값이 나타나는 변수는 종속변수에 비정상적인 영향을 주거나, 오차가 일정하지 않은 문제(이분산성)가 발생한다.   이런 경우 데이터 값을 변환(transformation)하는 것도 하나의 해결방법이 된다.  변환이란  데이터의 분포 형태를 바꾸는 것이라고 생각하면 된다. 사회과학에서는 그중에서도 로그(log)와 제곱근(sqrt) 변환이 가장 널리 사용된다. 로그 변환 –..

– 어떤 회귀모형을 쓸까?  회귀분석은 사회과학에서 인과관계를 분석할 때 매우 널리 사용된다.  분석 과정이 비교적 직관적이고, 결과 해석도 간명하기 때문이다.  특히 혼란변수(Confounder)를 통제하면서 특정 독립변수가 종속변수에 미치는 영향을 분석할 수 있다는 점에서 유용하다.하지만 회귀분석에는 생각보다 다양한 변형 기법이 존재하고, 이로 인해 분석 방법을 선택할 때 혼란을 겪는 경우도 많다. 그래서 이 글에서는 종속변수의 성격에 따라 어떤 회귀모형이 적절한지 정리보았다.논문을 읽을 때나 직접 분석할 때, 종속변수가 어떤 특성을 갖고 있는지, 그리고 그에 적합한 회귀모형은 무엇인지 살펴볼 필요가 있다.  회귀분석의  중요 가정: 종속변수의 분포기본적인 선형 회귀분석에서는 종속변수가 연속형이고  ..

회귀분석을 위해서는 독립변수의 약 10배 정도의 사례가 필요하다고 하지만,  더  작은 표본으로도 데이터의 패턴을 적절히 추출할 수 있다는 연구도 있다.  또한 연구자가 예상하는 효과 크기를 바탕으로 표본 수를 계산하여 정할 수 있다는 접근법도 존재한다.그러나 사회과학 분야에서 작은 표본이 가지는 위험성은 단순히 표본 크기가 작다는 점을 넘어서, 더 중요한 문제가 있을 수 있다. 따라서 표본 크기 자체 보다는 이 점을 확인해야 한다.사회과학 분야의 작은 표본은 대체로 무작위 표집(random sampling) 방식으로 전집에서 추출되지 않는 경우가 많고,  따라서 전집의 특성이 충분히 반영되지 않았을 가능성이 크다.  특히 독립변수의 변동성이 충분하지 않을 가능성이 높다. 예를 들어, 농장의 규모와 농장..