회귀분석을 할 때 연속형 변수는 대개 별다른 가공 없이 그대로 분석에 사용한다.
그러나 값의 범위가 너무 크거나, 분포가 한쪽으로 심하게 치우쳐 있는 경우에는 그대로 사용하기에 적합치 않다.
이런 변수를 그대로 쓰면 회귀모형의 가정을 위배하거나, 결과 해석이 왜곡될 수 있다.
예를 들어, 도시 인구, 기업 매출, 가구소득처럼 일부 극단적으로 큰 값이 나타나는 변수는 종속변수에 비정상적인 영향을 주거나, 오차가 일정하지 않은 문제(이분산성)가 발생한다. 이런 경우 데이터 값을 변환(transformation)하는 것도 하나의 해결방법이 된다. 변환이란 데이터의 분포 형태를 바꾸는 것이라고 생각하면 된다. 사회과학에서는 그중에서도 로그(log)와 제곱근(sqrt) 변환이 가장 널리 사용된다.
로그 변환 – 기하급수적 수치를 비율 중심으로
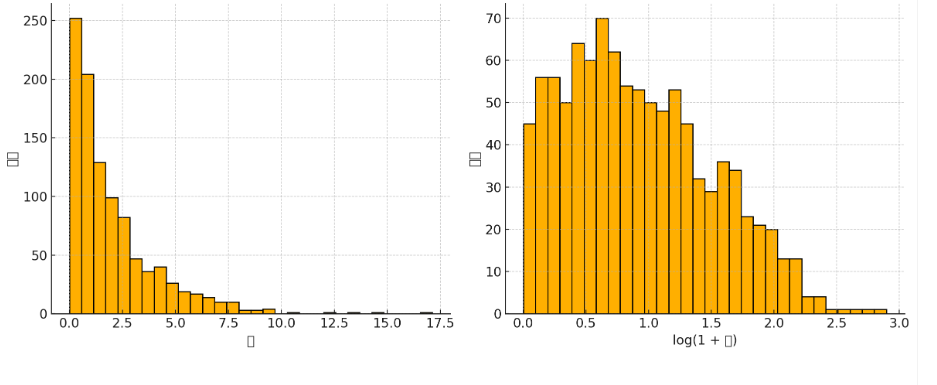
로그를 사용해서 값은 변환하면 큰 값이 더 많이 줄어든다. 아래의 왼쪽 그림의 데이터를 로그 변환하면 오른쪽 그림이 된다. 분포가 좌우 대칭에 가깝워 진다. 또한 로그 변환을 사용하면 해석방식도 비율방식으로 바뀌어야 한다. 예를 들어, 인구가 인구 1명 증가할 때 소득증가가 얼마이다는 방식 보다는 인구가 e배 증가했을 때 소득증가가 얼마이다는 방식이 더 자연스럽다. 도시규모가 차이가 많을 때 특히 유용하다.
제곱근 변환 – 완만한 치우침 보정
제곱근 변환은 로그 변환을 사용할 만큼 분포가 심하게 치우치지는 않았지만, 그러나 분포가 여전히 치우쳐 있어 정규화가 필요할 때 유용하다.
예를 들어, 사건 발생 횟수나 출석 일수처럼 대부분 값이 작고 0 이상인 경우, 로그를 취하면 너무 변화가 클 수 있다.
이럴 때 제곱근을 취하면 분포가 더 정규분포에 가까워지고, 회귀분석의 가정도 잘 충족시킨다.
아래에서 왼쪽의 데이터를 로그변환하면 가운데, 그리고 제곱근 변환을 적용하면 오른쪽이 된다.

- 이러한 변환은 종속변수, 독립변수 구분 없이 적용 가능하다.
- 다만 해당 변수만 변환하면 되고, 다른 변수까지 함께 변환할 필요는 없다.
- 중요한 것은 변환 후 해석도 변환된 기준에 맞게 달라진다는 점이다.
예컨대 로그를 썼다면, 회귀계수의 “1단위 증가”는 “e배 증가했을 때"와 같이 해석해야 한다.
'회귀분석' 카테고리의 다른 글
| 로지스틱 회귀분석 1 : 이진형(binary) 종속변수 (2) | 2025.04.10 |
|---|---|
| 회귀분석 계통도 0 - 하나의 가계도, 다양한 자손들 (0) | 2025.04.06 |
| 회귀분석 계통도 6- 베이지안 회귀 - 사전 지식과 소표본 (0) | 2025.04.06 |
| 회귀모형 계통도 5: 유연한 비선형 회귀- GAM, 스플라인 회귀 (0) | 2025.04.06 |
| 회귀분석 계통도4- 일부만 보이는 데이터: 절단, 검열, 선택, 구조적 0 (0) | 2025.04.05 |