로지스틱 회귀는 종속변수가 이진형(binary)일 때 사용하는 회귀분석 기법이다. 일반적인 선형 회귀는 결과 값이 연속형일 때 적합하지만, 로지스틱 회귀는 결과가 '성공/실패', '예/아니오', '1/0'처럼 두 가지 범주로 나뉘는 경우에 적절하다.
예를 들어, 교육 프로그램에 참여할 확률이나 투표 여부를 예측하는 데 사용할 수 있다.
1. 왜 로지스틱 회귀를 사용하는가?
선형 회귀분석을 이진형 종속변수에 사용하면 예측값이 0~1 범위를 벗어난다. 그래서 로지스틱 회귀는 독립변수의 선형 결합을 시그모이드 함수(logistic function)를 통해 변환하여 0과 1 사이의 값을 갖도록 한다.
이처럼 로지스틱 회귀는 비선형적으로 변환하는 과정을 거쳐 예측값을 산출하기 때문에 선형 회귀에 비해 해석이 다소 직관적이지 않다. 또한 결정계수(R²) 역시 일반 선형 회귀처럼 절대값으로 해석할 수 없고, 상대적으로 평가해야 한다.
로지스틱 회귀의 확률 추정식은 다음과 같다:
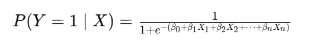
이 함수는 입력값이 커질수록 1에 가까워지고, 작아질수록 0에 가까워지는 S자형 곡선(sigmoid curve)을 따른다. 이를 로그 오즈(log-odds)의 선형 결합 형태로 바꾸면 다음과 같이 표현된다:
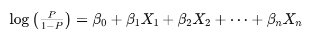
여기서 계수는 오즈비(odds ratio)의 로그값이며, 실제 해석에서는 지수변환을 통해 오즈비로 해석한다.
2. 해석 방법
로지스틱 회귀분석은 종속변수가 0과 1일 경우에 사용할 수 있기 때문에, 활용도가 높다. 그러나 예측된 종속변수 값이 확률이 아니라 로그 오즈(log odds)로 표현된다. 로그 오즈는 우리에게 익숙하지 않다. 그래서 그 지수값인 오즈비(odds ratio)로 바꾸어서 해석한다. 예를 들어, 독립변수인 성별에서 남자는 1, 여자는 0으로 코딩되어 있고, 해당 계수의 오즈비가 1.8로 계산되었다면 이는 남성이 여성보다 특정 사건이 발생할 가능성이 1.8배 높다는 의미다. 오즈비가 1보다 크면 해당 변수는 종속변수가 1인 가능성을 높이고, 1보다 작으면 낮추는 것으로 해석된다.
각 계수의 통계적 유의성은 유의확률(p-value)을 통해 판단하며, 일반적으로 p < 0.05일 경우 통계적으로 의미 있는 변수로 간주한다. p값은 Wald 통계량(Wald statistic)을 기반으로 계산된다. Wald 통계량은 각 회귀계수(β)가 0과 유의하게 다른지를 검정하기 위한 지표로, 다음과 같은 공식으로 산출된다:

이 값을 토대로 유의확률(p값)이 산출하여, 해당 변수가 결과에 유의미한 영향을 미치는지를 판단할 수 있다.
3. 회귀계수의 예시와 해석 방법
정당지지 여부를 예측한다고 하자. 종속변수는 정당지지 여부 (party: 1 = 지지, 0 = 반대)이고, 독립변수로는 나이(age), 성별(gender), 캠페인노출 경험(campaign_exposure)이 포함된다. 이러한 자료를 바탕으로 로지스틱 회귀모형을 사용하여 다음과 같은 결과를 얻었다고 가정하자.
| 변수 | 회귀계수 (β) | 오즈비 (exp(β)) | 유의확률 (p-value) |
| 나이 | 0.03 | 1.03 | 0.081 |
| 성별(여성) | 0.62 | 1.86 | 0.021 |
| 캠페인노출 | 1.15 | 3.16 | 0.004 |
나이의 계수는 0.03, 성별(여성)의 계수는 0.62, 캠페인노출의 계수는 1.15로 나타났다. 이 값들을 exp(β) 함수를 사용하여 exp(오즈비(odds ratio)로 환산하면 각각 1.03, 1.86, 3.16에 해당한다. (exp(0.03) = 1.03, exp(0.62)=1.86, exp(1.15)=3.16). SPSS 등의 통계패키지는 로지스틱 결과물에 exp(β) 값을 제공한다.
유의확률(p-value)을 보면, 캠페인 노출과 성별은 유의수준 0.05보다 작게 나와, 영향을 주는 것으로 해석된다. 나이는 유의수준보다 높은 값을 보여 영향이 없는 것으로 해석된다.
즉 다음과 같이 해석할 수 있다.
| 캠페인에 노출된 사람은 그렇지 않은 사람보다 지지할 오즈(odds)가 약 3.16배 더 높게 나타났다. 이는 캠페인 효과가 매우 강력하게 작용한다는 것을 보여준다. 여성은 남성보다 지지할 가능성이 약 1.86배 높았으며, 이 역시 유의하였다. 한편, 나이는 통계적으로 유의미한 영향을 미치지는 못하는 것으로 나타났다. |
일반선형회귀에서는 표준화계수의 값을 비교하여 변수의 중요성을 말하지만, 로지스틱에서는 위의 예시처럼 비표준화계수의 지수값(exp)으로 그 변수의 중요성을 판단한다. 오즈비가 1보다 크면 +의 영향을 - 면 부적인 영향을 준다.
3-2. 모델 적합도 해석
로지스틱 회귀분석의 모델 적합도는 선형 회귀에서처럼 하나의 결정계수(R²)로 요약되기 어렵다. 다양한 지표를 함께 사용하지만 대표적인 것으로는 다음과 같은 것들이 있다.
a. -2 Log Likelihood (-2LL):
작을수록 데이터에 잘 맞는 모형이다. 기준 모형(null model)에 비해 -2LL이 충분히 감소했다면 모형의 설명력이 향상된 것이다.
- 예시: 기준 모형 -2LL = 1432.8 → 완전 모형 -2LL = 1352.4 → 감소폭 = 80.4
b. 의사결정계수(Pseudo R²):
일반 선형 회귀의 R²와 유사한 지표로, Cox & Snell R² 또는 Nagelkerke R²가 자주 사용된다. Cox & Snell R² 는 아래 식에서 보듯이 선형회귀의 R²와 유사한 방식으로 정의되지만 최대값이 1보다 작다. 그리고 최대값이 1이 되도록 수정한 것이 Nagelkerke R²다. 그런데 이들은 모델 적합도가 얼마나 개선되었는가를 나타내는 것이지, R²처럼 변량을 설명한 정도를 나타내는 것이 아니다. 따라서 해석시에는 설명력이 높다 또는 낮다와 같이 절대적으로 해석하기 보다는 모형 간 상대적 비교로 해석한다. 예컨대 Nagelkerke R² = 0.114로 기준모형에 비해 일정 수준의 설명력을 가진다 정도로 해석할 수 있다. 여기서 기준모형이란 독립변수를 하나도 넣지 않고 종속변수만 예측하는 경우를 말하고 완전모형은 독립변수를 모두 넣은 모형을 말한다.

이것을 아래와 같이 최대값이 1이 되도록 수정한 것이 Nagelkerke R²다.
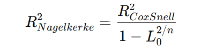
구체적으로 모형의 적합도는 다음과 같은 방식으로 해석할 수 있다.
| 분석 결과, 모델의 적합도를 나타내는 -2 Log Likelihood는 기준 모형(-2LL = 1432.8) 대비 완전 모형(-2LL = 1352.4)에서 크게 감소하였다. 해당 모형이 통계적으로 유의미하게 향상되었음을 시사한다. |
<로지스틱 회귀분석 2: 해석방법과 GPT 프롬프트> https://skcho.tistory.com/60 에서 계속됩니다>
'회귀분석' 카테고리의 다른 글
| 로지스틱 회귀분석 2: 해석방법과 챗지피티 프롬프트 (0) | 2025.04.10 |
|---|---|
| 회귀분석 계통도 0 - 하나의 가계도, 다양한 자손들 (0) | 2025.04.06 |
| 변수의 로그 변환과 제곱근 변환- '큰 수'를 현실적으로 만들기 (0) | 2025.04.06 |
| 회귀분석 계통도 6- 베이지안 회귀 - 사전 지식과 소표본 (0) | 2025.04.06 |
| 회귀모형 계통도 5: 유연한 비선형 회귀- GAM, 스플라인 회귀 (0) | 2025.04.06 |